
Pentru a afla cum să faci testul, înregistrează-te pe eduboom!
Înregistrează-te Ești înregistrat? Întră în cont »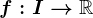 are proprietatea lui Darboux pe intervalul
are proprietatea lui Darboux pe intervalul  dacă oricare ar fi
dacă oricare ar fi 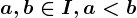 și oricare ar fi
și oricare ar fi 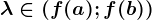 atunci ecuația
atunci ecuația  are cel puțin o soluție pe intervalul
are cel puțin o soluție pe intervalul  .
. este continuă pe intervalul
este continuă pe intervalul  atunci
atunci  are proprietatea lui Darboux pe
are proprietatea lui Darboux pe  .
. are o discontinuitate de prima speță pe intervalul
are o discontinuitate de prima speță pe intervalul  atunci
atunci  nu are proprietatea lui Darboux pe
nu are proprietatea lui Darboux pe  .
. are o discontinuitate de speța a doua pe intervalul
are o discontinuitate de speța a doua pe intervalul  atunci
atunci  nu are proprietatea lui Darboux pe
nu are proprietatea lui Darboux pe  .
.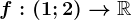 . Dacă
. Dacă 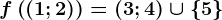 atunci
atunci  nu are proprietatea lui Darboux pe intervalul
nu are proprietatea lui Darboux pe intervalul  .
. atunci
atunci  are proprietatea lui Darboux pe intervalul
are proprietatea lui Darboux pe intervalul ![[1;3]](https://static.eduboom.ro/eduboom_ro/uploads/latex/cache/c/8/2/d/d/c82dd251f8d52ea71fdd1c2a5cc29501d8ed4a51.png) .
.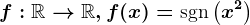 atunci
atunci  are proprietatea lui Darboux pe intervalul
are proprietatea lui Darboux pe intervalul 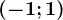 .
.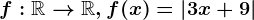 atunci
atunci  nu are proprietatea lui Darboux pe intervalul
nu are proprietatea lui Darboux pe intervalul ![[-4;-2]](https://static.eduboom.ro/eduboom_ro/uploads/latex/cache/5/7/a/7/5/57a753fa6dd90762085d36a08fcba935ca7d85e2.png) .
. . Studiază continuitatea funcției
. Studiază continuitatea funcției  și stabilește dacă are proprietatea lui Darboux pe
și stabilește dacă are proprietatea lui Darboux pe  .
.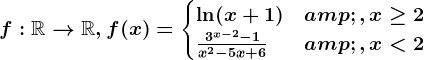 . Studiază continuitatea funcției
. Studiază continuitatea funcției  și stabilește dacă are proprietatea lui Darboux pe intervalul
și stabilește dacă are proprietatea lui Darboux pe intervalul  .
.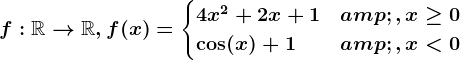 . Studiază continuitatea funcției
. Studiază continuitatea funcției  și stabilește dacă are proprietatea lui Darboux pe intervalul
și stabilește dacă are proprietatea lui Darboux pe intervalul ![\left [ -\frac12;\frac12 \right ]](https://static.eduboom.ro/eduboom_ro/uploads/latex/cache/c/5/5/6/4/c55645872204c1331a01b710a4cb9fec11627365.png) .
. . Studiază continuitatea funcției
. Studiază continuitatea funcției  și stabilește dacă are proprietatea lui Darboux pe intervalul
și stabilește dacă are proprietatea lui Darboux pe intervalul 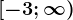 .
.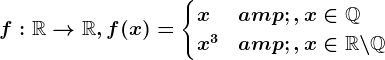 atunci
atunci  are proprietatea lui Darboux pe intervalul
are proprietatea lui Darboux pe intervalul ![\left ( \sqrt[3]26;\sqrt[3]28 \right )](https://static.eduboom.ro/eduboom_ro/uploads/latex/cache/d/5/a/c/d/d5acd1fdb7c1b3187a5b03de247ec94c707ebf6a.png) .
.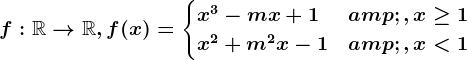 . Determină
. Determină  pentru care funcția
pentru care funcția  are proprietatea lui Darboux pe
are proprietatea lui Darboux pe  .
.
 . Determină
. Determină  pentru care funcția
pentru care funcția  are proprietatea lui Darboux pe
are proprietatea lui Darboux pe ![[0;4]](https://static.eduboom.ro/eduboom_ro/uploads/latex/cache/4/c/1/3/8/4c1386618e72df9c3e89c1de6174dff9a1e801d2.png) .
.
Descrierea testului
Verifică-ți cunoștințele despre proprietatea lui Darboux, cu acest test online de matematică pentru clasa a XI-a. Aici vei găsi probleme în care, folosind criteriile date în lecție, vei stabili dacă o funcție dată are sau nu această proprietate . Așa că nu mai sta pe gânduri, rezolvă testul ca să fii cel mai BOOM la mate!
Pentru a comenta acest test, fii parte din eduboom!