Test: Derivatele funcțiilor elementare. Partea II

Test

Întrebările pe care le vei întâlni în test:

Derivata funcției $f:\mathbbR--> \mathbbR$ , $f(x)=\cos x$ este:

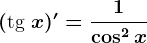Derivata funcției $\texttg x$ este dată de relația $(\texttg x)'=\frac1\cos^2x$ .

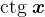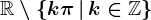Funcția $\textctg x$ este derivabilă pe mulțimea $\mathbbR\setminus \left \ k\pi \,|\,k\in\mathbbZ \right \$ și $\left (\textctg x \right )'=\frac1\sin^2x$ .

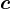Fie constanta reală $c$ și funcția derivabilă $f$ . Atunci $(c\cdot f)'=c'\cdot f'$ .

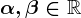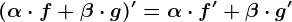Dacă $f$ și $g$ sunt funcții derivabile și numerele $\alpha ,\beta \in \mathbbR$ , atunci $(\alpha \cdot f+\beta \cdot g)'=\alpha \cdot f'+\beta \cdot g'$ .

Asociază funcțiile de mai jos cu derivatele corespunzătoare.

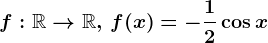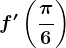Se consideră funcția $f:\mathbbR--> \mathbbR,\,f(x)=-\frac12\cos x$ . Calculează $f'\left ( \frac\pi 6 \right )$ .

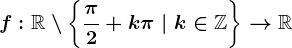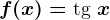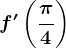Se dă funcția $f:\mathbbR\setminus \left \ \frac\pi 2+k\pi \mid k\in \mathbbZ \right \--> \mathbbR$ cu $f(x)=\texttg x$ . Calculează $f'\left ( \frac\pi 4 \right )$ .

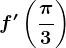Se consideră funcția $f:\mathbbR\setminus \left \ k\pi \mid k\in \mathbbZ \right \--> \mathbbR,\, f(x)=\frac14\textctg x$ . Atunci $f'\left ( \frac\pi 3 \right )$ este egal cu: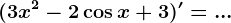

$(3x^2-2\cos x+3)'=...$

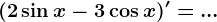
$(2\sin x-3\cos x)'=...$

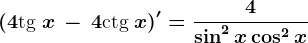Este adevărat că $\left ( 4\texttg x \, -\, 4\textctg x \right )'=\frac4\sin^2x\cos^2x$ ?

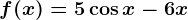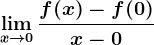Fie funcția $f:\mathbbR--> \mathbbR$ , $f(x)=5\cos x -6x$ . Calculează valoarea limitei $\limx--> 0\fracf(x)-f(0)x-0$ .

Răspunde cu număr format din cifre și eventual semnul minus.

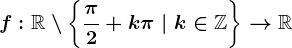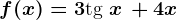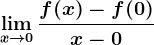Se consideră funcția $f:\mathbbR\setminus \left \ \frac\pi 2+k\pi \mid k\in \mathbbZ \right \--> \mathbbR$ , $f(x)=3\texttg x\,+4x$ . Calculează valoarea limitei $\limx--> 0\fracf(x)-f(0)x-0$ .

Completează răspunsul cu număr format din cifre.

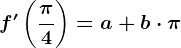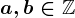Se consideră funcția $f:\mathbbR\setminus \left \ k\pi \mid k\in \mathbbZ \right \--> \mathbbR,\, f(x)=3\textctg x\,+2x^2$ . Dacă $f'\left ( \frac\pi 4 \right )=a+b\cdot \pi$ cu $a,b\in \mathbbZ$ , determină numerele $a$ și $b$ .

Completează răspunsurile folosind numere formate din cifre și eventual semnul minus.

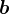Descrierea testului

Derivatele funcțiilor elementare. Partea II, analiză matematică clasa a XI-a, este tot un test cu derivatele elementare, unde te vei confrunta din ce în ce mai mult cu formule de derivare prezentate în lecția video. Rezolvând acest test vei înțelege foarte bine aceste noțiuni și vei avea rezultatele dorite atât la școală cât și la examenele care te așteaptă. Mult succes!

Pentru a comenta acest test, fii parte din eduboom!

Intră în contul tău! Înregistrează-te

Comentarii (0)