
Pentru a afla cum să faci testul, înregistrează-te pe eduboom!
Înregistrează-te Ești înregistrat? Întră în cont » , unde
, unde 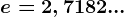 este un număr irațional, baza logaritmului natural.
este un număr irațional, baza logaritmului natural. , putem afirma că
, putem afirma că  ?
? , atunci
, atunci 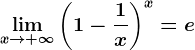 ?
? , atunci
, atunci  ?
? și
și 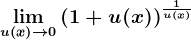 , prin înlocuire vei obține nedeterminare de tipul ...
, prin înlocuire vei obține nedeterminare de tipul ...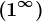 , vei transforma expresia așa încât să o aduci la una din formele:
, vei transforma expresia așa încât să o aduci la una din formele: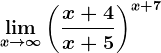 , vei modifica baza și o vei scrie sub forma...
, vei modifica baza și o vei scrie sub forma...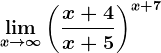 , vei modifica baza și exponentul puterii și vei scrie expresia de sub limită sub forma...
, vei modifica baza și exponentul puterii și vei scrie expresia de sub limită sub forma...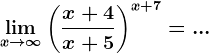

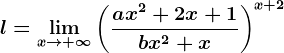 , cu
, cu 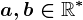 .
.
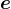 .
. sau
sau 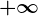 , scrie în cuvinte, folosind litere mici și un singur spațiu între cele două cuvinte.
, scrie în cuvinte, folosind litere mici și un singur spațiu între cele două cuvinte.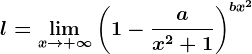 , unde
, unde 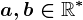 .
.
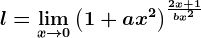 , cu
, cu 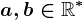 .
.
Descrierea testului
Vei lucra acum un nou test de la analiza matematică de clasa a XI-a - aici vei verifica ce ai înțeles despre cum modelezi un exercițiu, atunci când întâlnești nedeterminarea de tipul 1 la infinit la calculul unei limite de funcții. Da, e puțin mai dificil, dar dacă urmezi pașii din lecția video, vei găsi de fiecare dată rezolvarea corectă. Fii atent/ă la etape, la calcule și la semne, eu îți urez succes și te aștept la testul următor.
Pentru a comenta acest test, fii parte din eduboom!